A personal finance question that is asked on many accounting and financial professional exams is the Lifetime Savings Problem, in which one is asked how much one would have to set aside on a regular basis, beginning in one’s youth, in order to enjoy a retirement of a particular level. A typical example is:
Imagine that you planned to retire 30 years from now, and that you wanted to set up an account, into which you would make equal-sized payments each year during your working years, that would enable you buy an annuity that would pay you $25,000 at the end of each year for the 25 years immediately after you retired. Based on the expectation that your savings account should earn 9% per annum and that the retirement annuity should have a more conservative yield to maturity of 3% per annum, how much should you set aside each year until your planned retirement?”
This problem is in two parts: a) your retirement plan, and b) your savings plan to achieve that goal.
Savings Plan
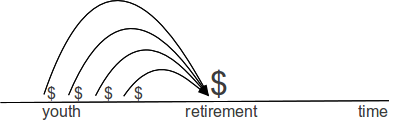
Pay into Retirement Account
Retirement Plan

Draw from Retirement Account
A financial arrangement like the ones depicted above, in which payments—called coupon payments (c) for historical reasons—are made on a regular schedule for a specified period of time (t) is known as an annuity*. Here, the retirement account is an annuity that will pay you (perhaps, you will buy it from an insurance company or a large bank), and the savings account is an annuity that you will pay into (perhaps, a brokerage account or a statutory retirement account that you manage with the help of a financial professional).
To solve this puzzle you need to work backwards, first by deciding how much you would like to receive each year after you retire and for how many years; then by calculating the expected value—the price that you expect to pay, when the time comes—of an annuity that will provide for your retirement, which value becomes your savings goal; and finally by calculating how much money you should set aside each year between now and retirement, in order to achieve that goal.
Before you can know how much (c) to pay each year into a savings account that you open in your early years, you need to know how much you want to save. In other words, the price (APV for “annuity present value”) of the annuity that you plan to buy when you retire—the price that you expect to have to pay upon retirement—is exactly equal to the amount that you need save (AFV for “annuity future value”) during your working years. Tomorrow’s present value (i.e., price) is today’s future value.
Retirement Plan
If you imagined, for planning purposes, that you could live on $25,000 (c) per year after you retire, and that you wanted to plan for a 25-year (t) retirement—on the expectation that you’ll figure out a Plan B sometime during the next 55 years, in case you live beyond Year 26 after retirement—and that you expected your retirement account to earn 3% (r) per year, then you would need to save (APV):
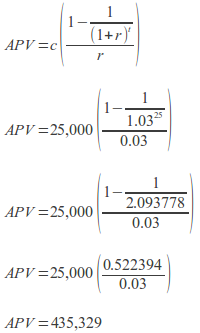
This means that you need to have $435,329 on the day of your retirement, 30 years from now, so that you can buy the annuity that will pay $25,000 per year for 25 years.
Savings Plan
In order to save that amount (AFV), you plan to make equal annual payments (c) for the next 30 years (t), and you expect that you can earn an average of 9% per year (r) over that time.

If all goes according to plan, then, if you set aside $3,194 at the end of every year for the next 30 years and earn an average of 9% per year on your savings, then you should have $435,329 in three decades that you can use to buy an annuity that pays $25,000 per year for 25 years.
Invest accordingly.
Prof. Evans
note: For a detailed explanation of annuities, review my “Time Value of Money” video lecture. If you have difficulty viewing the videos try using VLC Media Player, “a free and open source cross-platform multimedia player and framework that plays most multimedia files as well as DVD, Audio CD, VCD, and various streaming protocols.” [return to main text]